教養の物理~4/23・5/7分
・最後の摩擦の関係が解らなかった
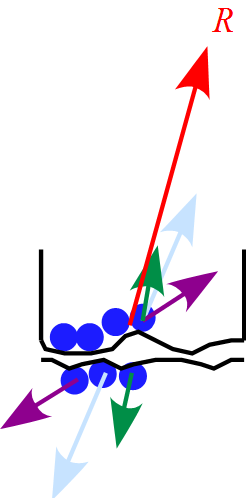
・抗力Rがよくわからなかった
抗力$R$は接触している面から受ける力です。
この面から受ける力は、接触面を拡大してみると
面を構成している分子間に働く電気的な力(分子間力)が作用しています。
この一つ一つを考えるのは大変なので、その合力を一つの力として考えたものが
抗力$R$となります。
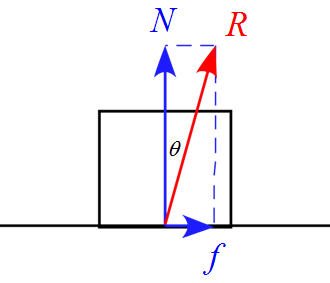
この抗力$R$を分解したものが垂直抗力$N$と摩擦力$f$になります。
・抗力$R$の垂直方向の成分 = 垂直抗力
・抗力$R$の水平方向の成分 = 摩擦力
摩擦係数については、
\begin{eqnarray*}
\tan \theta = \frac{f}{N} = \mu
\end{eqnarray*}
と定義されています。
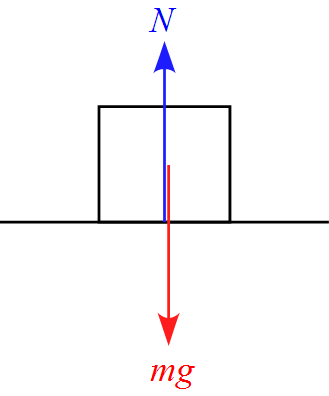
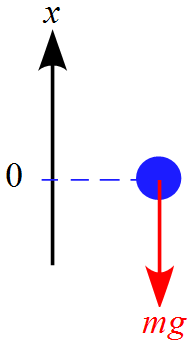
よく、台に置かれた物体のモデルにおいて、
重力$mg$の反作用として$N$があると
思っている人が居ますが、それは間違いです。
このモデルにおいて物体に作用する力は、重力$mg$と抗力$R$の2つです。
垂直方向の運動方程式は上向きを正とすると
\begin{eqnarray*}
ma=N-mg
\end{eqnarray*}
となります。
物体は垂直方向には移動しないので、$a=0$となり、
\begin{eqnarray*}
0&=&N-mg \\
N&=&mg
\end{eqnarray*}
となります。
従って、運動方程式の結果から$N=mg\ $が言えます。
しかしこれは作用反作用の関係ではありません。
作用反作用の法則は
\begin{eqnarray*}
\mbox{地球が物体を引く力の大きさ} &=& \mbox{物体が地球を引く力の大きさ} \\
\mbox{物体が床から受ける抗力の大きさ } &=& \mbox{床が物体から受ける抗力の大きさ }
\end{eqnarray*}
です。
抗力と重力の関係については述べていません。
抗力と重力の関係が判るのは運動方程式から導かれるものです。
・自由落下のエネルギー保存則について
自由落下のモデルで力学的エネルギーが保存することはよく知られています。
これを示す方法をいくつか紹介します。
・力学的エネルギーを計算した結果が定数であることを示す
運動エネルギー$K=\frac{1}{2}mv^2$
位置エネルギー$U=mgx$
の$v$や$x$を求めて、$K,U$をそれぞれ計算し、その合計を計算する。
・運動方程式を変形して力学的エネルギーが時間に依存しないことを示す。
・運動方程式を$x$で積分して力学的エネルギーが定数になる事を示す。
それぞれについて考えてみると
・力学的エネルギーを計算した結果が定数であることを示す
上向きを正に軸を取り、物体に作用する力は重力$mg$であるから
運動方程式は
\begin{eqnarray*}
ma=-mg\\
m\frac{dv}{dt}=-mg
\end{eqnarray*}
である。
\begin{eqnarray*}
\frac{dv}{dt}=-g
\end{eqnarray*}
より、
\begin{eqnarray*}
\frac{dv}{dt}&=&-g \\
v&=&-gt+C
\end{eqnarray*}
初速度は無い自由落下なので$t=0$で$v=0$より
\begin{eqnarray*}
v(0)=-g\cdot 0+C &=&0 \\
C&=&0
\end{eqnarray*}
よって
\begin{eqnarray*}
v(t)=-gt
\end{eqnarray*}
さらに、$x$は
\begin{eqnarray*}
v= \frac{dx}{dt} &=&-gt \\
x &=& -gt^2 \cdot \frac{1}{2} +C'
\end{eqnarray*}
原点スタートとすると、$t=0$で$x=0$より
\begin{eqnarray*}
x(0)=-\frac{1}{2} g \cdot 0^2 +C' &=&0 \\
C' &=&0
\end{eqnarray*}
よって
\begin{eqnarray*}
x(t)=-\frac{1}{2}gt^2
\end{eqnarray*}
これで準備ができたので$K,U$に代入すると
運動エネルギー$K$は
\begin{eqnarray*}
K(t)=\frac{1}{2}mv^2 &=& \frac{1}{2}m (-gt)^2 \\
&=& \frac{1}{2} mg^2 t^2
\end{eqnarray*}
位置エネルギー$U$は
\begin{eqnarray*}
U(t)=mgx &=& mg \Bigl( -\frac{1}{2}gt^2 \Bigr) \\
&=& -\frac{1}{2} mg^2 t^2
\end{eqnarray*}
よって、力学的エネルギー$E$は
\begin{eqnarray*}
E(t)=K(t)+U(t) &=& \frac{1}{2} mg^2 t^2 + \Bigl( -\frac{1}{2} mg^2 t^2 \Bigr) \\
&=& 0
\end{eqnarray*}
と定数になり、力学的エネルギーが保存していることになります。
・運動方程式を変形して力学的エネルギーが時間に依存しないことを示す。
運動方程式は
\begin{eqnarray*}
m\frac{dv}{dt}=-mg
\end{eqnarray*}
である。
この両辺に$v=\frac{dx}{dt}$をかけると
\begin{eqnarray*}
m\frac{dv}{dt} \cdot v &=& -mg\frac{dx}{dt} \\
\frac{d}{dt} \Bigl( \frac{1}{2}mv^2 \Bigr) &=& -\frac{d}{dt}(mgx) \\
\frac{d}{dt} \Bigl( \frac{1}{2}mv^2 + mgx \Bigr ) &=& 0
\end{eqnarray*}
この$(\ \ \ )$内は運動エネルギーと位置エネルギーの合計になっていて、
それを時間で微分するとゼロになる事を表しています。
時間で微分するとゼロになるということは、
$(\ \ \ )$内は時間に依存しない値であることを表しています。
従って、力学的エネルギーは時間に依らず一定であり、保存していると言えます。
・運動方程式を$x$で積分して力学的エネルギーが定数になる事を示す。
運動方程式は
\begin{eqnarray*}
m\frac{dv}{dt}=-mg
\end{eqnarray*}
である。
この式を$x$で積分すると
\begin{eqnarray*}
\int m\frac{dv}{dt} dx &=& \int -mg dx \\
\int m\frac{dv}{dt} v dt &=& \int -mg dx \\
\int m v dv &=& \int -mg dx \\
\frac{1}{2}mv^2 &=& -mgx +C'' \\
\frac{1}{2}mv^2 +mgx &=&C''
\end{eqnarray*}
この状態でも$C''$は定数なので力学的エネルギーは保存していると言えますが、
初期条件より、$t=0$で$v=0,x=0$であるので
\begin{eqnarray*}
E(0)=\frac{1}{2}m \cdot 0^2 + mg \cdot 0 &=&C'' \\
C'' &=&0
\end{eqnarray*}
となります。
従って、
\begin{eqnarray*}
E(t)=\frac{1}{2}mv^2 + mgx &=& 0 \\
\end{eqnarray*}
となるので、力学的エネルギーは保存している。
いずれの方法も理解し、身に着けておきましょう。