・イメージが難しいです。
・イメージする図形が何をイメージすればいいのか分からない。
・空間内部の電気量というのがよく分からない。
・内部の電気量の考え方が分からない。イメージするのが難しい。
・電気量が何故$\frac{4}{3}\pi R^3 \rho $になるのかが分かりません。
まず、2つの段階に分けて考える必要があると思います。
1. 内部の電気量に相当する部分はどの部分までか?を考える
2. 一様の密度で分布している場合に置いて、その内部の部分の電気量はどのように表されるのか?
この2つです。
同時に考えようとすると混乱するかもしれません。
段階を踏んでガウスの法則を適用させてみて下さい。
物体内に一様に密度$\rho$で分布している場合の電気量は
\begin{eqnarray*}
Q=\mbox{体積} \times \rho
\end{eqnarray*}
になります。
・コンデンサーの静電エネルギーで$W=\frac{1}{2}QV$の$\frac{1}{2}$が
何故出てくるのか分かりません。
面積を求めた時、(積分をした時)に出てきます。
コンデンサーの静電エネルギーは$V-Q$グラフの面積から求めることができます。
$Q=CV$より$V=\frac{1}{C}Q$となり、静電容量$C$は定数であるため、
$V$と$Q$は比例関係になります。
つまり、$V-Q$グラフでは直線になります。
従って、$Q=0$から$Q=Q$までの間の静電エネルギーは
\begin{eqnarray*}
U=W=\frac{1}{2}QV
\end{eqnarray*}
となります。
積分から求める場合は
\begin{eqnarray*}
U=W &=& \int_{0}^{Q} VdQ \\
&=& \int_{0}^{Q} \frac{1}{C} Q dQ\\
&=& \frac{1}{2}\frac{Q^2}{C} \\
\end{eqnarray*}
となります。
この式に$Q=CV$を代入すれば$\frac{1}{2}QV$の形も出てきます。
・線電荷を用いた例題の類似問題も解説して欲しい。
ヒントを掲載したのでそれを参考に解いてみて下さい。
・ガウスの法則の考え方がイマイチ理解できませんでした。
・ちょっと何言ってるのか分からないです。
ガウスの法則について復習してみましょう。
ガウスは、単位面積当たり$E$ [本]~その場所の電場と同じ本数~の
電気力線が通過していると考えた。
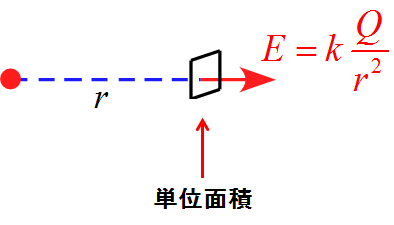
例えば、点電荷$Q$があったとする。
ここから$r$だけ離れた場所に単位面積を考えると
この単位面積を貫く電気力線の本数は、この場所の電場と同じ本数であるから、
\begin{eqnarray*}
\mbox{単位面積を貫く本数} = E = k \frac{Q}{r^2}
\end{eqnarray*}
となる。
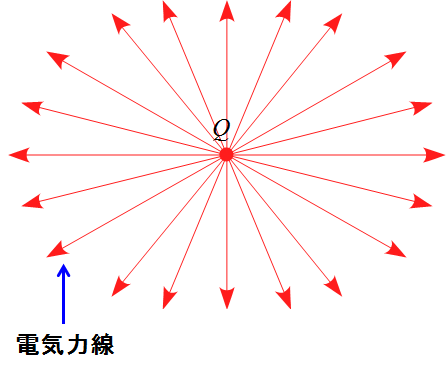
点電荷$Q$からは電気力線が放射状に出ている。
この点電荷$Q$から出ている電気力線の本数は何本になるか考えてみよう。
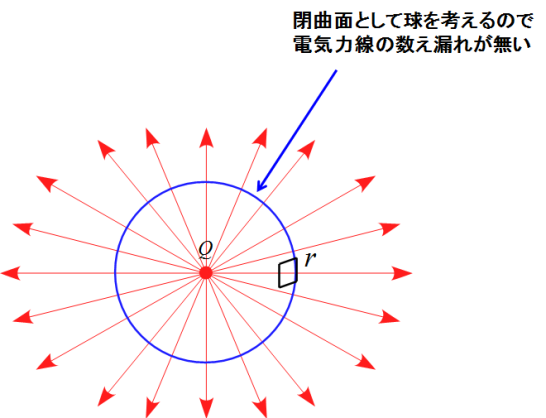
点電荷$Q$から出る電気力線の数え漏れをなくすために、
閉曲面として半径$r$の球を考える。
この球を貫く電気力線の本数が点電荷$Q$から出てくる電気力線の全本数になる。
ガウスは単位面積当たり$E$ [本]の電気力線が貫くと考えたので、
球を貫く電気力線の本数は
\begin{eqnarray*}
\mbox{電気力線の本数} = \mbox{電場} E \times \mbox{球面の面積}
\end{eqnarray*}
である。
よって、
\begin{eqnarray*}
\mbox{全電気力線の本数} = k \frac{Q}{r^2}\times 4\pi r^2 = 4\pi k Q \ [\mbox{本}]
\end{eqnarray*}
となる。
ここで、この本数$4\pi k Q$は$r$が含まれていない。
これが意味することは、$r$に依存しないあたりであるため、
「帯電している物体の形状に依存しない」ということである。
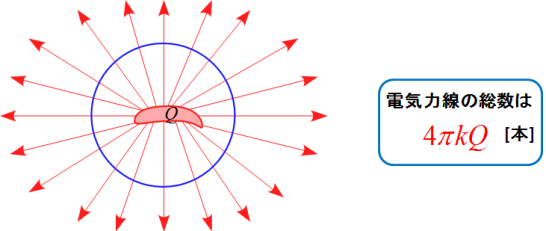
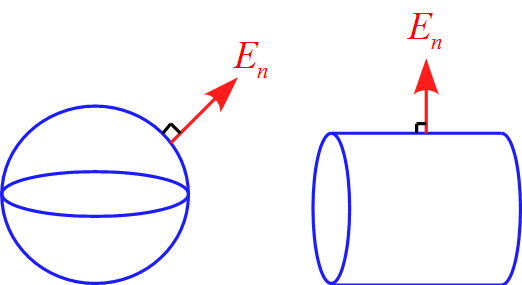
つまり、今は点電荷$Q$について考えたが、点である必要はなく、
例えば、
こんな変な形でも、帯電している電気量が$Q$であれば
この物体からでる電気力線の全本数は$4\pi k Q$ [本]である。
クーロン定数$k$を$k=\frac{1}{4\pi \varepsilon _0}$と書き換えると、
\begin{eqnarray*}
\mbox{全電気力線の本数} = 4\pi k Q = 4\pi \frac{1}{4\pi \varepsilon _0} Q = \frac{Q}{\varepsilon _0}\ [\mbox{本}]
\end{eqnarray*}
と表すことができる。
ざっくり書くと
\begin{eqnarray*}
\mbox{閉曲面を垂直な電場} \times \mbox{閉曲面の表面積} = \frac{\mbox{閉曲面内部の電気量}}{\varepsilon _0}
\end{eqnarray*}
と考えることができます。
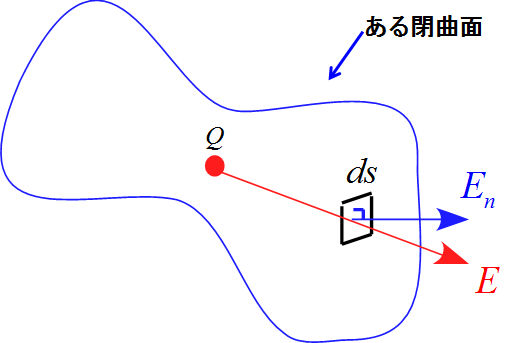
ざっくり書きすぎたので、細かく見ていくと
今は半径$r$の球を閉曲面としてイメージしたが、
一般的に考えると、
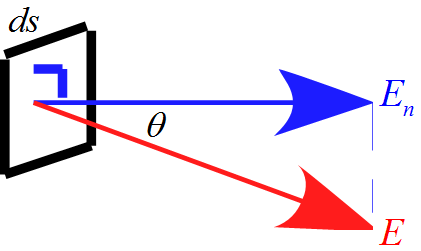
微小面積$ds$部分は
\begin{eqnarray*}
\mbox{閉曲面を垂直な電場} \times \mbox{閉曲面の表面積} = E_n ds
\end{eqnarray*}
となる。
これを全閉曲面に対して積分(合計)すると、
\begin{eqnarray*}
\int_{S}E_n ds
\end{eqnarray*}
と表すことになります。
これが全電気力線の本数$\frac{Q}{\varepsilon _0}$になるので
\begin{eqnarray*}
\int_{S}E_n ds = \frac{Q}{\varepsilon _0}
\end{eqnarray*}
と表すことができます。
これをガウスの法則(積分形)と呼びます。
ここで$Q$は閉曲面内部の電気量を表しています。
点電荷であれば単に$Q$で良いのですが、
ある密度で電荷が分布している場合はそれぞれについて計算する必要が出てきます。
線密度$\rho$の場合
\begin{eqnarray*}
Q= \int_{l} \rho dl
\end{eqnarray*}
面密度$\sigma$の場合
\begin{eqnarray*}
Q= \int_{s} \sigma ds
\end{eqnarray*}
体積密度$\rho$の場合
\begin{eqnarray*}
Q= \int_{V} \rho dV
\end{eqnarray*}
を計算することになります。
密度が一定の場合は
\begin{eqnarray*}
Q= \int_{l} \rho dl = \rho l
\end{eqnarray*}
\begin{eqnarray*}
Q= \int_{s} \sigma ds =\sigma s
\end{eqnarray*}
\begin{eqnarray*}
Q= \int_{V} \rho dV = \rho V
\end{eqnarray*}
となります。